En probabilidad, el concepto de variable aleatoria es uno de los pilares fundamentales para entender el comportamiento de un fenómeno aleatorio ya que su comportamiento está gobernado por una función de distribución $F_X(x)$.

Sin embargo en ocasiones es complicado visualizar el comportamiento de dicha variable aleatoria, por lo que es necesario simular valores que podría tomar una realización de dicha variable aleatoria.

En este artículo se presenta una forma de simular valores de una distribución usando números aleatorios.

Método para simular variables aleatorias

La técnica para simular variables aleatorias es la transformación integral de probabilidad. Esta técnica nos dice que para generar valores de una variable aleatoria $X$ con función de de distribución $F_X(x)$, es suficiente con generar valores aleatorios $u$ de una función de distribución uniforme en el intervalo (0,1) y hacer \(x = F_X^{-1}(u).\)

Las computadoras (e incluso calculadoras) tienen generadores de números aleatorios que pueden servir para crear valores de $x$.

Para mayores detalles se puede consultar (Mood, Graybill, y Boes 1974).

Ejemplo de números aleatorios

Supóngase que se quieren simular valores de una distribución exponencial con parámetro $\lambda \gt 0$, es decir \(F_X(x)=(1-e^{-\lambda x})I_{(0,\infty)}(x).\)

Para generar valores de esta distribución, basta con hacer \(x = -(1/\lambda)\log (1-u).\)

Ejemplo con R

El siguiente código en R muestra una forma de realizarlo. La forma de generar los números aleatorios es mediante la función aleat_exp(). Esta función usa valores generados de números aleatorios uniformes por medio de la función de R runif(), se hace la transformación y devuelve un resultado.

Cuando se llama la función, el resultado se almacena en el vector x y posteriormente se crea el dataframe simulacion para poder graficar su histograma.

#Función para simular
aleat_exp <- function(n,l=1) {
  u = runif(n)
  x = (-1/l)*log(1-u)
  return(x)
}
x = aleat_exp(1000,5)
simulacion = data.frame(X =x)
#Gráfica
library(ggplot2)
ggplot(data = simulacion,aes(X))+geom_histogram()+theme_classic()+
  labs(y="Conteo",title = "Simulación de una variable aleatoria exponencial")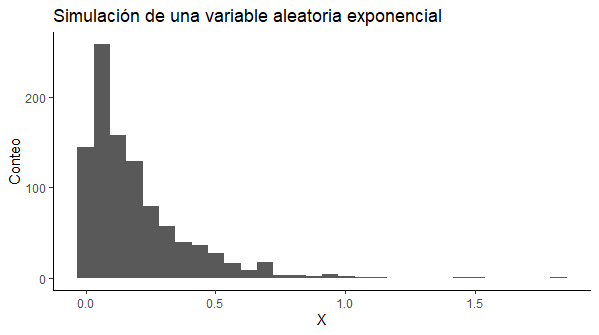

Histograma de la simulación con R

Si se desea replicar el resultado, antes de llamar la función se puede usar la función set.seed() indicando la semilla con el fin de poder replicar el resultado, por ejemplo set.seed(123).

Ejemplo con SAS software

Se ejemplifica la forma de crear valores aleatorios usando SAS/STAT® software.

Primero se definen las variables macro a usar &n. y &lambda., posteriormente se usa un paso data para crear un dataset con los números aleatorios generados y finalmente se grafican con el procedimiento proc sgplot.

/*Variables macro*/
%LET n = 1000;
%LET lambda = 5;
data simulacion;
    do i = 1 to &n.;
       u = rand("uniform");
       x = (-1/&lambda.)*log(1-u);
       output;
    end;
    keep x;
run;
/*Gráfico*/
proc sgplot data=simulacion;
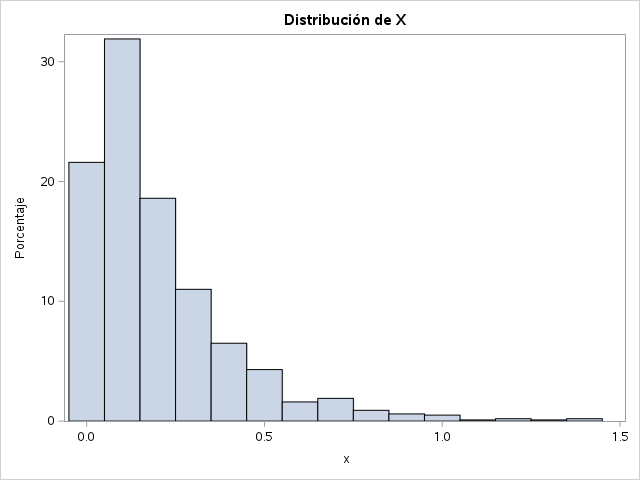
  histogram x;
  title "Distribución de X";
run;

Para establecer un valor inicial de la secuencia, se puede usar la llamada a la rutina call streaminit; antes de generar los números aleatorios, por ejemplo call streaminit(12345);.

Histograma de la simulación con SAS

Ejemplo con Julia

Para generar números aleatorios con Julia, se puede definir una función y después se puede graficar usando la función histogram del paquete StatsPlot.

    function rand_exp(n,l=1)
        u = rand(n)
        x = -1*(1/l)*log.(1 .- u)
        return x
    end
    x = rand_exp(1000,5)
    using StatsPlots
    histogram(x,xlabel="X", ylabel="Frecuencia",legend =:none)
    title!("Distribución de X")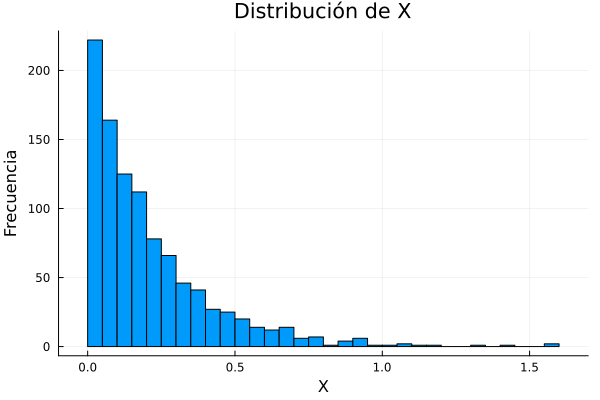

Histograma de la simulación con Julia

Para establecer una semilla inicial se puede usar la función Random.seed!() de la librería Random, por ejemplo, Random.seed!(123).

Ejemplo en Python

En Python, se puede definir una función para generar los números aleatorios y posteriormente se puede graficar su comportamiento. Se requiere la librería numpy para el generador de números aleatorios y mathplotlib para los gráficos.

import numpy as nu
from numpy.random import uniform
import matplotlib.pyplot as mp

def rand_exp(n, l=1):
    x = [0]*(n)
    u = uniform(low=0, high=1, size=n)
    x = (-1/l)*nu.log(1-u)
    #x = nu.array(x)
    return x

x = rand_exp(1000, 5)

mp.hist(x)
mp.title('Distribución de $X$')
mp.show()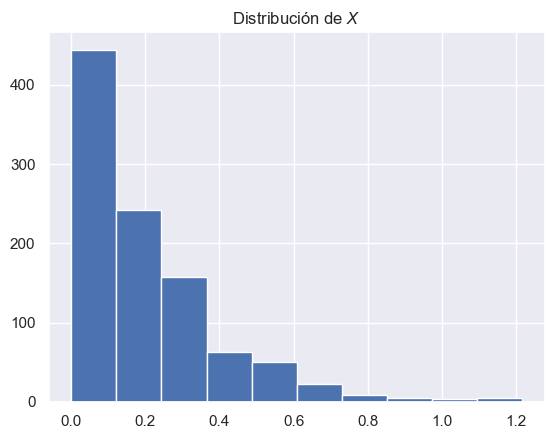

Histograma de la simulación con Python

Para establecer un valor inicial, se puede usar la función numpy.random.default_rng(), por ejemplo numpy.random.default_rng(seed=123).

Conclusión

Esta técnica es muy útil para simular valores con cierta distribución y es muy fácil de usar. Sin embargo, no siempre será fácil encontrar \(F_X^{-1}(u)\) y se requerirán técnicas más avanzadas.

En el próximo artículo exploraremos otras técnicas para simular variables aleatorias de otras distribuciones, por ejemplo la distribución normal.

Referencias

Nazarathy, Yoni, y Hayden Klok. 2021. Statistics with Julia. Switzerland: Springer.

Mood, Alexander, Franklin Graybill, y Duane Boes. 1974. Introduction to the Theory of Statistics. McGraw-Hill.

R Core Team. 2022. R: A language and environment for statistical computing. R Foundation for Statistical Computing. https://www.R-project.org/.

SAS Institute Inc. 2018. SAS/STAT 15.1 User’s Guide. Cary, NC.

SAS and all other SAS Institute Inc. product or service names are registered trademarks or trademarks of SAS Institute Inc. in the USA and other countries. ® indicates USA registration.