Algoritmo Gibbs sampler
En estadística Bayesiana es de interés conocer la distribución a posteriori, es decir:
\[f(\theta|x) \propto f(X|\theta)f(\theta)\]donde $\mathbf{\theta}$ es un vector de parámetros de dimensión $k$ y $x$ representa los datos.
Sin embargo, en ocasiones obtener esta densidad es compilcada, por lo que se deben recurrir a técnicas numéricas.
Una de estas técnicas es el algoritmo de Gibbs o muestrador de Gibbs (Hoff 2009). Este método en un algoritmo iterativo que consiste en obtener muestras de las distribuciones condicionales completas de la siguiente manera:
Dada una sucesión de valores $\mathbf{\theta}^{(i)}=(\theta_1^{(i)},\theta_2^{(i)},\dots,\theta_k^{(i)})^t$ se simula de la siguiente manera:
1.- Simular de las distribuciones condicionales completas:
\[\begin{align*} \theta_1^{(i+1)} &\sim f(\theta_1|x,\theta_2^{(i)},\dots,\theta_k^{(i)})\\ \theta_2^{(i+1)} &\sim f(\theta_2|x,\theta_1^{(i+1)},\theta_3^{(i)}\dots,\theta_k^{(i)})\\ \vdots\\ \theta_k^{(i+1)} &\sim f(\theta_k|x,\theta_1^{(i+1)},\theta_2^{(i+1)}\dots,\theta_{k-1}^{(i+1)}) \end{align*}\]2.- Repetir desde el paso 1 hasta obtener convergencia.
Note que este algoritmo requiere especificar cada una de las distribuciones condicioneales completas y se deben especificar valores iniciales y algún criterio de paro.
Ejemplo de aplicación
El siguiente ejemplo muestra el funcionamiento del algoritmo Gibb sampler para el caso de la regresión lineal.
El modelo de regresión lineal múltiple describe la relación entre una variable respuesta $Y_i$ y un conjunto de covariables $X_1,X_2,\dots,X_p$. El modelo se puede describir de la siguiente manera:
\[\begin{align} Y_i = \beta_0+\beta_1 X_{i1}+\beta_2 X_{i2} + \dots + \beta_p X_{ip} + e_i \end{align}\]donde $\boldsymbol{\beta} = (\beta_0,\beta_1,\dots,\beta_p)^t$ son los parámetros de interés (desconocidos) y $e_i$ es una variable aleatoria normal independiente e idénticamente distribuída con media 0 y varianza $\sigma^2$ (desconocida).
Note que es de interés conocer tanto la media como la varianza de $Y_i$ condicionada a los valores $x_{i1}, x_{i2},\dots, x_{ip}$. Se puede demostrar fácilmente que $E(Y_i|x_{i}) = \beta_0+\beta_1 x_{i1}+\beta_2 x_{i2} + \dots + \beta_p x_{ip}$ y $V(Y_i|x_{i}) = \sigma^2$.
Bajo estas condiciones, es de interés estimar los parámetros desconocidos $\boldsymbol{\beta}$ y $\sigma^2$.
Una forma de estimar los parámetros de interés es usando inferencia bayesiana. Este enfoque asume que los parámetros de interés son variables aleatorias cuya distribución $p(\theta)$, llamada distribución a priori, es conocida.
En este paradigma, es de interés conocer la distribución a posteriori de los parámetros dados los datos, mediante el teorema de Bayes.
\[\begin{align} p(\theta|x)=\frac{p(\theta)p(x|\theta)}{p(x)}\propto p(\theta)f_{\mathbf{Y}}(\mathbf{y}|\mathbf{x},\boldsymbol{\beta},\sigma^2) \end{align}\]Note que para el caso de regresión lineal se puede deducir que la distribución condicional de $Y_i$ es
\[f_{Y_i}(y_i|x_i,\boldsymbol{\beta},\sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}}e^{\frac{-1}{2 \sigma^2} (y_i-\mathbf{x}_i\boldsymbol{\beta})^2}\]Si $Y_i$ son independientes, entonces, la distribución conjunta es:
\[\begin{align} f_{\mathbf{Y}}(\mathbf{y}|\mathbf{x},\boldsymbol{\beta},\sigma^2) = \left(\frac{1}{\sqrt{2\pi \sigma^2}}\right)^ne^{\frac{-1}{2 \sigma^2} \sum_{i=1}^n (y_i-\mathbf{x}_i\boldsymbol{\beta})^2} \end{align}\]Si se asume distribuciones a priori no informativa, es decir total desconocimiento a cerca del comportamiento de los parámetros, se puede porponer la siguiente distribución:
\[p(\boldsymbol{\theta})=p(\boldsymbol{\beta})p(\sigma^2)\propto \frac{1}{\sigma^2}\]se puede demostrar que la función de distribución a posteriori los parámetros es
\[p(\boldsymbol{\beta}|\mathbf{x},\mathbf{y},\sigma^2)\propto e^{-\frac{1}{2\sigma^2}\left(\boldsymbol{\beta} -\hat{\boldsymbol{\beta}} \right)^t\mathbf{X}^t \mathbf{X}\left(\boldsymbol{\beta} - \hat{\boldsymbol{\beta}}\right)}\]donde $\boldsymbol{\beta}=(\mathbf{X}^t \mathbf{X})^{-1}\mathbf{X}^t \mathbf{y}$ y la varianza del error
\[p(\sigma^2|\boldsymbol{\beta},\mathbf{x},\mathbf{y})\propto \left(\frac{1}{\sigma^2}\right)^{\frac{n+2}{2}}e^{-\frac{1}{2\sigma^2}\left(\mathbf{y} -\mathbf{X}\boldsymbol{\beta} \right)^t\left(\mathbf{y} - \mathbf{X}\boldsymbol{\beta}\right)}\]Por lo tanto, se concluye que:
\[\begin{align} p(\boldsymbol{\beta}|\mathbf{x},\mathbf{y},\sigma^2) &= N_p\left(\hat{\boldsymbol{\beta}},\sigma^2(\mathbf{X}^t \mathbf{X})^{-1}\right)\\ p(\sigma^2|\boldsymbol{\beta},\mathbf{x},\mathbf{y}) &= IG(n/2,\left(\mathbf{y} -\mathbf{X}\boldsymbol{\beta} \right)^t\left(\mathbf{y} - \mathbf{X}\boldsymbol{\beta}\right)/2) \end{align}\]Se pueden consultar más detalles sobre la derivación de las distribuciones a posteriori en este enlace.
Para obtener muestras de $\boldsymbol{\beta}$ y $\sigma^2$ se puede usar el siguiente procedimiento:
- Establecer valores iniciales $\boldsymbol{\beta}^{(i=0)}$ y $\sigma^2_{(i=0)}$.
- Simular valores para $\sigma^2_{(i)}$.
- Simular valores para $\boldsymbol{\beta}^{(i)}$ usando $\sigma^2_{(i)}$.
- Repetir los pasos 2 y 3 hasta obtener un número grande de muestras.
La base de datos utilizada para el ejemplo fue obtenida de kaggle y consiste en información del salario anual de cierta compañia en función de años de experiencia, nivel de educación género y grado de estudios; para fines ilustrativos, únicamente se tomará en cuenta la variable años de experiencia.
Nota: La base original contenía la variable salario medida en dólares, sin embargo por razones de redondeo se dividió entre 1000 para que la interpretación sea expresada en miles de dólares anuales, se encontrón un registro con un valor de 350 dólares anuales, basándose en observaciones con características similares, se asumió que fue un error en la captura de los datos por lo que se consideró el valor 35000, esta base modificada puede descargarse de este link.
Debido a que no se tiene información a priori y se tiene un tamaño de muestra grande, se puede asumir una distribución a priori no informativa, es decir $p(\mathbf{\theta})\propto \frac{1}{\sigma^2}$, por lo que se tendrían resultados similares a la estimación por máxima verosimilitud.
Ejemplo con R
Primero se puede estimar los parámetros simulando de la distibución a posteriori.
# Datos
datos = read.csv("https://fcoavc.github.io/assets/SalaryData.csv")
y = datos$Salary
X = model.matrix(~YearsExperience,datos)
n = length(y)
XtX = t(X) %*% X
inv_XtX = solve(XtX)
# valores iniciales
m = 2000
beta_ini = rep(0, ncol(X))
betas_post = matrix(0,nrow=m,ncol=ncol(X))
sigma2_post = matrix(0,nrow=m, ncol=1)
# algoritmo
library(MASS)
set.seed(123)
for(i in -1000:m){
ri = y - X %*% beta_ini
sigma2_ini = 1 / rgamma(1, n/2, sum(ri ^ 2)/2)
Sigma = sigma2_ini*inv_XtX
beta_ini = mvrnorm(n=1, inv_XtX%*%t(X)%*%y, Sigma)
if(i>=1){
sigma2_post[i] = sigma2_ini
betas_post[i, ] = beta_ini
}
}Los resultados se muestran a continuación.
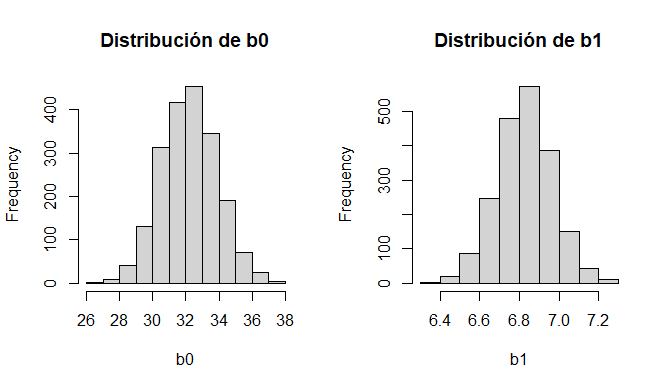
par(mfrow=c(1,2))
hist(betas_post[,1],main = "Distribución de b0",xlab="b0")
hist(betas_post[,2],main = "Distribución de b1",xlab="b1")
medias_post = apply(betas_post, 2, mean)
names(medias_post) <- names(beta_ini)
medias_post
lm(Salary~YearsExperience,datos)> medias_post
(Intercept) YearsExperience
32.205503 6.826937
> lm(Salary~YearsExperience,datos)
Call:
lm(formula = Salary ~ YearsExperience, data = datos)
Coefficients:
(Intercept) YearsExperience
32.199 6.826
Ejemplo con SAS software
Debido a que se realizarán cálculos iterativos, se debe trabajar con SAS/IML 15.1. El siguiente código muestra cómo implementar el algoritmo, primero se leen los datos y se crea la matriz diseño.
/* Lectura de datos*/
FILENAME web URL "https://fcoavc.github.io/assets/SalaryData.csv";
PROC IMPORT OUT = salary DATAFILE = web DBMS = CSV REPLACE;
GETNAMES = YES;
DATAROW = 2;
GUESSINGROWS=1000;
RUN;
/* Matriz diseño */
proc transreg data=salary design;
model identity(salary) = identity(yearsexperience);
output out=diseno;
run;Posteriormente se leen los datos y se simula usando el algoritmo de Gibbs.
proc iml;
use work.diseno;
read all var {salary} into y;
read all var {intercept yearsexperience} into x;
close work.diseno;
n = nrow(y);
nmc = 2000;
betas_post = j(nmc,2,.);
sigma2_post = j(nmc,1,.);
betas0 = {0,0};
XtX = t(X) * X;
inv_XtX = inv(XtX);
call randseed(123);
DO i = -1000 TO nmc;
eta = X*betas0;
ri = y-eta;
sce = sum(ri##2);
sigma20 = 1/randfun(1,"Gamma",n/2,2/sce);
V = sigma20#inv_XtX;
mu = inv_XtX*t(X)*y;
betas1 =RandNormal( 1, mu, v);
IF i>=1 then DO;
sigma2_post[i] = sigma20;
betas_post[i,] = betas1;
END;
END;
mbetas = mean(betas_post);
msigma2 = mean(sigma2_post);
MATTRIB mbetas COLNAME = {"beta 0" "beta 1"};
print "Media posterior betas", mbetas;
create posterior from betas_post[colname={"beta0" "beta1"}];
append from betas_post;
close posterior;
quit;Finalmente se procesan los datos resultantes para presentar una gráfica.
data posterior;
set posterior;
i = _N_;
run;
proc transpose data=posterior out = betas(rename=(_name_ = coef)) prefix=beta;
by i;
var beta0 beta1;
run;
data betas;
set betas;
label coef = "Parámetro";
run;
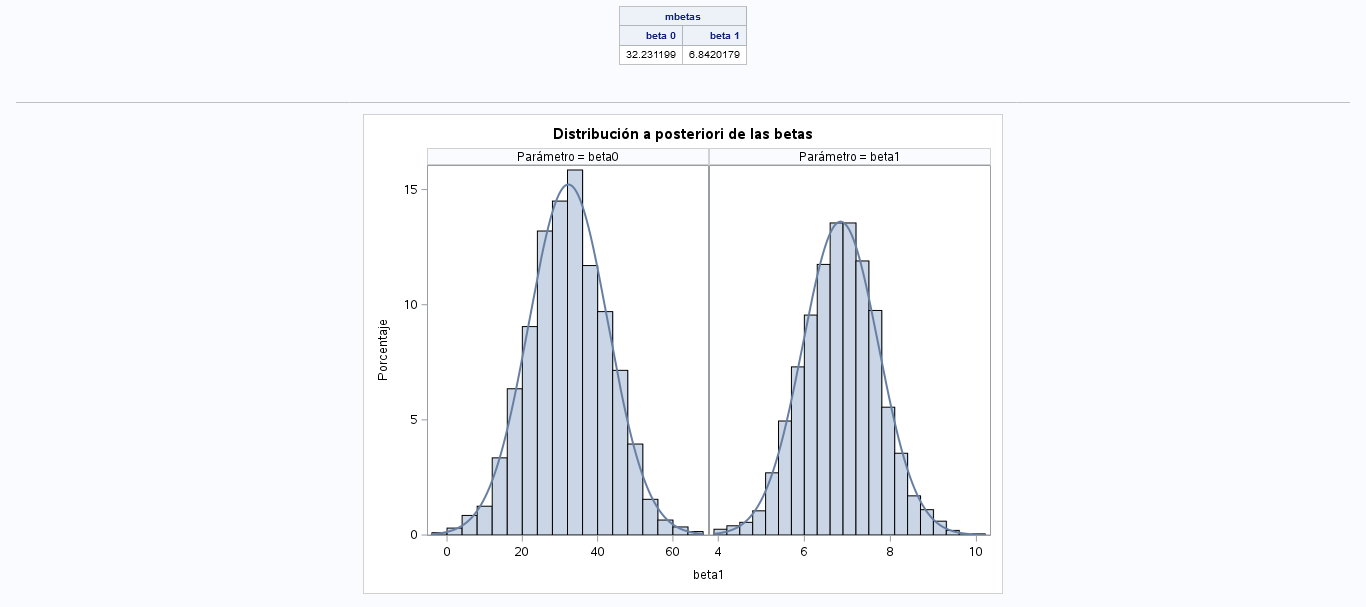
proc sgpanel data=betas noautolegend;
title "Distribución a posteriori de las betas";
panelby coef /UNISCALE= ROW;
histogram beta1;
density beta1;
run;
title;El resultado se muestra a continuación.
Referencias
Hoff, Peter. 2009. A First Course in Bayesian Statistical Methods. New York: Springer.