Optimización de funciones con Newton-Raphson
En inferencia estadística es de interés conocer el Estimador de Máxima Verosimilitud, es decir, un estimador que maximice la función de verosimilitud. Sin embargo, salvo en pocos casos, no es posible encontrar un estimador de forma analítica, por lo que es necesario recurrir a métodos numéricos. Una forma de encontrar una estimación que maximice la función de verosimilitud es mediante el algoritmo Newton-Raphson.
El método de Newton-Raphson es una técnica numérica para encontrar las raíces de una función (Burden & Faires, 2002), es decir, los valores de $x$ tal que $f(x)=0$. La idea básica es aproximarse “actualizando” los valores obtenidos anteriormente hasta encontrar una solución aproximada, si es posible hallarla.
La fórmula para encontrar la raíz de la función es la siguiente:
\[x^{(i) }=x^{(i−1) }−\frac{f\left(x^{(i−1) }\right)}{f´\left(x^{(i−1) } \right) }\]El algoritmo se describe a continuación.
Datos de entrada: valor inicial x0, tolerancia tol, número de iteraciones niter.
1.- Tomar i=1
2.- Mientras i<=niter hacer
3.- Calcular x=x0-f(x0)/f’(x0)
4.- Si |x-x0|<tol entonces regresa x y finaliza satisfactoriamente.
5.- Tomar i=i+1
6.- Tomar x0=x
7.- Fin Mientras
8.- Salida. El método no logró encontrar una solución.
9.- Fin del programa.
Se requiere de un valor inicial $x^{(0)}$ para iniciar con la búsqueda y que la función $f(x)$ sea derivable.
Una ventaja importante de este algoritmo es que puede aplicarse a funciones multivariadas.
Implementación del algoritmo
En muchas aplicaciones estadísticas, se requiere encontrar el valor $\hat{\theta}$ que maximice el logaritmo de la verosimilitud $l(\theta)$, por lo que los valores de $\hat{\theta}$ se encuentran mediante la búsqueda de las raíces de la derivada de la log-verosimilitud o función score $S(\theta)$ y con el negativo de la segunda derivada $H(\theta)$ o Hessiano. Note que en este caso se requiere que la función de log-verosimilitud sea 2 veces derivable con respecto a $\theta$.
La fórmula para encontrar una estimación del vector de parámetros que maximiza la función de log-varosimilitud es la siguiente.
\[\hat{\theta}^{(i) }=\hat{\theta}^{(i−1) }+H\left(\hat{\theta}^{(i−1) }\right)^{-1} S\left(\hat{\theta}^{(i−1) } \right)\]El método de Newton-Raphson no solo sirve para encontrar estimaciones puntuales de los parámetros, sino que es posible obtener una estimación de la varianza de los estimadores usando la inversa del negativo del hessiano o también llamada Información de Fisher, por lo que este método es útil para construir un intervalo de confianza usando las propiedades del estimador de máxima verosimilitud.
Ejemplo de aplicación
Los datos para el siguiente ejemplo fueron tomados de Meeker y Escobar (1998). Supóngase que se tienen datos de un experimento en el cual se registró el tiempo de falla hasta las 5 mil horas de cierto dispositivo a distintas temperaturas. Para este ejercicio, se omitirán los tiempos con censura y únicamente se considerarán observaciones cuya temperatura fue de 80 °C.
Si se asume que los tiempos de falla $T_1,\dots, T_n$ se ajustan a una distribución Weibull, su función de distribución está dada por
\[f_T(t;\gamma,\beta) = \frac{\gamma}{\beta}\left( \frac{t}{\beta}\right) ^{\gamma-1}e^{-\left( \frac{t}{\beta}\right)^\gamma }\;t,\beta ,\gamma > 0\]Es de interés estimar los parámetros $\gamma$ y $\beta$, donde $\gamma$ es el parámetro de forma y $\beta$ es el parámetro de escala.
Puede mostrarse que la función de log-verosimilitud es la siguiente:
\[l(\gamma,\beta) = n (\log \gamma - \gamma \log \beta) + (\gamma - 1) \sum_{i=1}^{n} \log t_i - \frac{\sum_{i=1}^{n}t_i^\gamma}{\beta^\gamma}\]Para utilizar el algoritmo Newton-Raphson, se requiere encontrar la función Score.
\[S(\gamma,\beta)=\begin{pmatrix} \frac{\partial l(\gamma,\beta)}{\partial \beta}\\ \frac{\partial l(\gamma,\beta)}{\partial \gamma} \end{pmatrix}\]donde
\[\frac{\partial l(\gamma,\beta)}{\partial \beta} = \frac{-n\gamma}{\beta} + \gamma \left( \frac{1}{\beta}\right)^{\gamma + 1} \sum_{i=1}^{n}t_i^\gamma\]y
\[\frac{\partial l(\gamma,\beta)}{\partial \gamma} = n \left(\frac{1}{\gamma} - \log \beta\right) + \sum_{i=1}^n \log t_i - \frac{\sum_{i=1}^{n}t_i^\gamma \log t_i + \log\frac{1}{\beta} \sum_{i=1}^{n}t_i^\gamma}{\beta ^{\gamma}}\]Así como el Hessiano
\[H(\gamma,\beta) = \begin{pmatrix} \frac{\partial^2 l(\gamma,\beta)}{\partial \beta^2} & \frac{\partial^2 l(\gamma,\beta)}{\partial \beta \partial \gamma} \\ \frac{\partial^2 l(\gamma,\beta)}{\partial \beta \partial \gamma} & \frac{\partial^2 l(\gamma,\beta)}{\partial \gamma^2} \end{pmatrix}\]donde
\[\frac{\partial^2 l(\gamma,\beta)}{\partial \beta^2} = \frac{n\gamma}{\beta^2} - \gamma(\gamma + 1) \left( \frac{1}{\beta}\right)^{\gamma + 2} \sum_{i=1}^{n}t_i^\gamma\],
\[\frac{\partial^2 l(\gamma,\beta)}{\partial \beta \partial \gamma} =- \frac{n}{\beta} +\frac{\gamma \sum_{i=1}^{n}t_i^\gamma \log (t_i) + \left( 1+\gamma \log \frac{1}{\beta} \right) \sum_{i=1}^{n}t_i^\gamma}{\beta ^{\gamma+1}}\]y
\[\frac{\partial^2 l(\gamma,\beta)}{\partial \gamma^2} = -\frac{n}{\gamma^2} - \frac{\sum_{i=1}^{n}t_i^\gamma \log (t_i)^2 + 2 \log\frac{1}{\beta} \sum_{i=1}^{n}t_i^\gamma\log t_i + \log \left( \frac{1}{\beta}\right)^2 \sum_{i=1}^{n}t_i^\gamma}{\beta ^{\gamma}}\]Finalmente la matriz de covarianzas puede ser estimada con $V(\gamma,\beta) = H(\gamma,\beta)^{-1}$.
Para iniciar con el algoritmo, se propone como valores iniciales el promedio simple para $\beta$ y se fijará $\gamma = 1$.
A continuación se mostrará cómo implementar este algoritmo en distintos lenguajes de programación.
Ejemplo con R
Primero se puede definir 3 funciones que serán de utilidad, la primera será la función de log-verosimilitud, la segunda la función score y por último la función hessiana.
Es recomendable que las funciones reciban un vector como argumento, mientras que los datos pueden ser definidos de forma global.
# Datos
ti = c(283,361,515,638,854,1024,1030,1045,1767,1777,1856,1951,1964,2884)
# Función de log-verosimilitud
logv = function(params){
beta = params[1]
gama = params[2]
n = length(ti)
s1 = n*(log(gama) - gama*log(beta));
s2 = (gama-1)*sum(log(ti));
s3 = (sum((ti^gama)))/(beta^gama);
s = s1+s2-s3;
return(s)
}
# Función score
score <- function(params) {
b = params[1]
g = params[2]
n = length(ti)
s1 = -n*g/b+g*sum(ti^g)*(1/b)^(g+1)
s2 = n*(1/g-log(b))+sum(log(ti))-(sum(ti^g*log(ti))+log(1/b)*sum(ti^g))/(b^g)
s = c(s1,s2)
return(s)
}
# Matriz hessiana
hessiano <- function(params) {
n = length(ti)
beta = params[1];
gama = params[2];
h11 = n*gama/beta^2 - gama*(gama+1)*(1/beta)^(gama+2)*sum((ti^gama));
h12 = -n/beta + (gama*sum((ti^gama)*log(ti)) + (1+gama*log(1/beta)) *
sum((ti^gama))) / (beta^(gama+1));
h22 = -n/gama^2 - (sum((ti^gama)*log(ti)^2) + 2*log(1/beta) *
sum((ti^gama)*log(ti)) + log(1/beta)^2*sum((ti^gama)))/(beta^gama);
h = matrix(c(h11,h12,h12,h22),nrow = 2,ncol = 2,byrow = TRUE)
return(h)
}Para la implementación del algoritmo, se pueden definir una función que reciba como argumentos los valores iniciales.
NR <- function(semilla,niter = 30, tol = 0.0001) {
inicial = semilla;
lvi = logv(inicial);
dist = 1;
i = 0;
while (i <= niter) {
H = hessiano(inicial);
VC = solve(H);
S = score(inicial);
final = inicial - VC%*%S;
dist = max(abs(final-inicial));
a = final[1];
b = final[2];
#hist = rbind(hist,cbind(i,dist,a,b));
if(dist < tol){
cat("Convergencia exitosa\n")
logv = logv(final);
grad = score(final);
VC = -solve(H);
cat("Log-verosimilitud final\n",logv,"\nValor del gradiente final\n",grad,
"\nMatriz de covarianzas estimada\n",VC,"\n Valores estimados\n")
#print(hist)
return(final);
}
i = i+1;
inicial = final;
}
cat("El algoritmo Newton-Raphson podría no converger\n",
"Se encontraron problemas de convergencia\n",
"El algoritmo fue detenido");
}
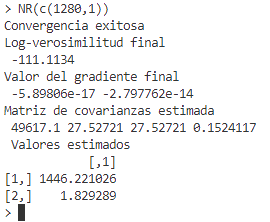
NR(c(1280,1))En la siguiente imagen se muestra el resultado del algoritmo.
Ejemplo con SAS software
Se ejemplifica la forma de estimar los parámetros aleatorios usando SAS® software.
Es importante mencionar que se debe trabajar con SAS/IML 15.1, debido a que se manejarán matrices.
Primero se invocará el procedimiento IML y se creará un vector que contengan los datos, posteriormente se crearán los módulos para la log-verosimilitud, función score y el hessiano.
Finalmente se implementará el algoritmo Newton-Raphson en un módulo que llamará las funciones antes definidas.
PROC IML;
/* Datos */
n = 14;
ti = {283 361 515 638 854 1024 1030 1045 1767 1777 1856 1951 1964 2884};
/* Función de verosimilitud */
START lvero (params) global (ti, n);
beta = params[1];
gama = params[2];
s1 = n#(log(gama) - gama#log(beta));
s2 = (gama-1)#sum(log(ti));
s3 = (sum((ti##gama)))/(beta##gama);
s = s1+s2-s3;
RETURN(s);
FINISH;
/*Score*/
START score (params) global (ti, n);
beta = params[1];
gama = params[2];
s1 = -n#gama/beta + gama#(1/beta)##(gama+1)#sum((ti##gama));
s2 = n#(1/gama-log(beta)) + sum(log(ti)) -(sum((ti##gama) # log(ti)) +
log(1/beta)#sum((ti##gama)))/(beta##gama);
s = s1 // s2;
RETURN(s);
FINISH;
START hessiano(params) GLOBAL (ti, n);
beta = params[1];
gama = params[2];
h11 = n#gama/beta##2 - gama#(gama+1)#(1/beta)##(gama+2)#sum((ti##gama));
h12 = -n/beta + (gama#sum((ti##gama)#log(ti)) + (1+gama#log(1/beta)) #
sum((ti##gama))) / (beta##(gama+1));
h22 = -n/gama##2 - (sum((ti##gama)#log(ti)##2) + 2#log(1/beta) #
sum((ti##gama)#log(ti)) + log(1/beta)##2#sum((ti##gama)))/(beta##gama);
h = ( h11 || h12) // (h12 || h22);
RETURN (h);
FINISH;
/* Algoritmo Newton - Raphson*/
START NR(semilla) GLOBAL (ti, n, niter, tol);
TITLE "Estimación de parámetros usando el Algoritmo Newton-Raphson";
inicial = semilla;
dist = 1;
i = 0;
DO WHILE(i <= niter);
H = hessiano(inicial);
VC = INV(H);
S = score(inicial);
final = inicial - VC*S;
dist = MAX(ABS(final-inicial));
a = final[1];
b = final[2];
history = history // (i || dist || a || b);
IF (dist < tol) THEN DO;
MATTRIB final ROWNAME = {"Beta","Gama"} LABEL = "Estimaciones";
message = "Convergencia exitosa";
MATTRIB message LABEL = "Status de convergencia";
PRINT message;
PRINT final;
logv = lvero(final);
grad = score(final);
MATTRIB logv LABEL = "Log-verosimilitud final";
MATTRIB grad LABEL = "Valor del gradiente final";
PRINT logv;
PRINT grad;
H = -Hessiano(final);
VC = INV(H);
MATTRIB VC LABEL = "Matriz de covarianzas estimada";
PRINT VC;
MATTRIB history COLNAME = {"Iteración","Distancia","Beta","Gama"}
LABEL = "Iteración";
PRINT history;
return;
END;
i = i+1;
inicial = final;
END;
ultiter = history[i,];
MATTRIB ultiter COLNAME = {"Iteración","Distancia","Beta","Gama"}
LABEL = "Última iteración";
message = {"El algoritmo Newton-Raphson podría no converger",
"Se encontraron problemas de convergencia",
"El algoritmo fue detenido"};
MATTRIB message LABEL = "Status de convergencia";
PRINT message,ultiter;
FINISH;
/* Valor inicial */
x0 = {1282,1};
niter = 25;
tol = 0.0001;
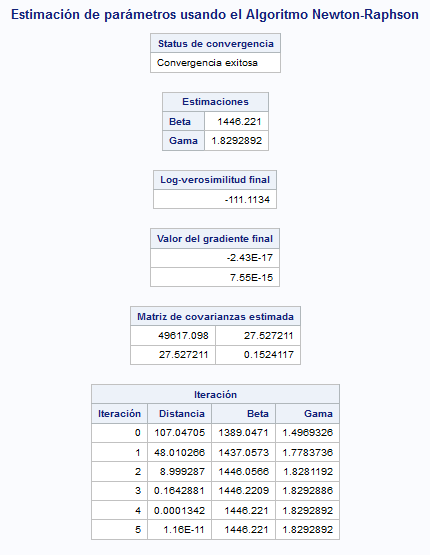
CALL NR (x0);
quit;La siguiente imagen muestra el resultado obtenido.
Ejemplo con Julia
Para optimizar una función con Julia con el algoritmo Newton-Raphson, primero se debe definir las funciones auxiliares y posteriormente se calculan los nuevos valores de forma iterativa.
# Datos
ti = [283,361,515,638,854,1024,1030,1045,1767,1777,1856,1951,1964,2884]
n = length(ti)
# Función de verosimilitud
function lvero(params)
beta = params[1]
gama = params[2]
s1 = n*(log(gama) - gama*log(beta))
s2 = (gama-1)*sum(log.(ti))
s3 = (sum((ti.^gama)))/(beta^gama)
s = s1+s2-s3
return s
end
# Función score
function score(params)
b = params[1]
g = params[2]
s1 = -n*g/b+g*sum(ti.^g)*(1/b)^(g+1)
s2 = n*(1/g-log(b))+sum(log.(ti))-(sum(ti.^g.*log.(ti))+log(1/b)*sum(ti.^g))/(b^g)
s = [s1,s2]
return s
end
# Matriz hessiana
function hessiano(params)
beta = params[1]
gama = params[2]
h11 = n*gama/beta^2 - gama*(gama+1)*(1/beta)^(gama+2)*sum((ti.^gama))
h12 = -n/beta + (gama*sum((ti.^gama).*log.(ti)) + (1+gama*log(1/beta)) *
sum((ti.^gama))) / (beta^(gama+1))
h22 = -n/gama^2 - (sum((ti.^gama).*log.(ti).^2) + 2*log(1/beta) *
sum((ti.^gama).*log.(ti)) + log(1/beta)^2*sum((ti.^gama)))/(beta^gama)
h = [[h11,h12] [h12,h22]]
return h
endPara la implementación del algoritmo Newton Raphson, se puede definir una función que reciba como argumentos los valores iniciales.
function NR(semilla,niter = 30, tol = 0.0001)
inicial = semilla
lvi = lvero(inicial)
dist = 1
i = 0
while i <= niter
H = hessiano(inicial)
VC = inv(H)
S = score(inicial)
final = inicial - VC*S
dif = abs.(final-inicial)
dist = dif[argmax(dif)]
if dist <= tol
println("Convergencia exitosa")
logv = lvero(final)
grad = score(final)
VC = -inv(H)
println("Log-verosimilitud final\n",logv,"\nValor del gradiente final\n",grad,
"\nMatriz de covarianzas estimada\n",VC,"\n Valores estimados\n")
return(final)
end
i = i+1
inicial = final
end
println("El algoritmo Newton-Raphson podría no converger\n",
"Se encontraron problemas de convergencia\n",
"El algoritmo fue detenido")
end
inicial = [1280,1]
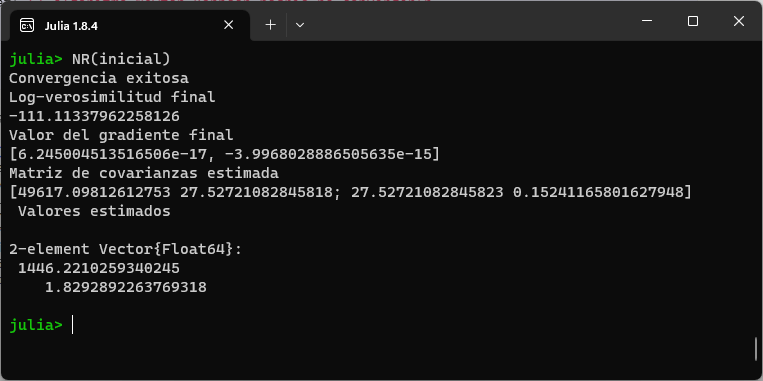
NR(inicial)En la siguiente imagen se ilustra el resultado del algoritmo.
Ejemplo con Python
Para optimizar una función con Python usando el algoritmo Newton-Raphson, primero se debe definir las funciones auxiliares y posteriormente se calculan los nuevos valores de forma iterativa.
# Datos
import numpy as nu
ti = nu.array([283,361,515,638,854,1024,1030,1045,1767,1777,1856,1951,1964,2884])
n = len(ti)
# Función de verosimilitud
def lvero(params):
beta = params[0]
gama = params[1]
s1 = n*(nu.log(gama) - gama*nu.log(beta))
s2 = (gama-1)*sum(nu.log(ti))
s3 = (sum((ti^gama)))/(beta^gama)
s = s1+s2-s3
return s
# Función score
def score(params):
b = params[0]
g = params[1]
s1 = -n*g/b+g*sum(ti**g)*(1/b)**(g+1)
s2 = n*(1/g-nu.log(b))+sum(nu.log(ti))-(sum(ti**g*nu.log(ti))+nu.log(1/b)*sum(ti**g))/(b**g)
s = nu.array([s1,s2])
return s
# Matriz hessiana
def hessiano(params):
beta = params[0]
gama = params[1]
h11 = n*gama/beta**2 - gama*(gama+1)*(1/beta)**(gama+2)*sum((ti**gama))
h12 = -n/beta + (gama*sum((ti**gama)*nu.log(ti)) + (1+gama*nu.log(1/beta)) *
sum((ti**gama))) / (beta**(gama+1))
h22 = -n/gama**2 - (sum((ti**gama)*nu.log(ti)**2) + 2*nu.log(1/beta) *
sum((ti**gama)*nu.log(ti)) + nu.log(1/beta)**2*sum((ti**gama)))/(beta**gama)
h = nu.array([[h11,h12], [h12,h22]])
return hA continuación se muestra el algoritmo Newton-Raphson.
from numpy.linalg import inv
def NR(semilla,niter = 30, tol = 0.0001):
inicial = semilla
lvi = lvero(inicial)
dist = 1
i = 0
while i <= niter:
H = hessiano(inicial)
VC = inv(H)
S = score(inicial)
final = inicial - VC@S
dist = max(nu.absolute(final-inicial))
if dist <= tol:
print("Convergencia exitosa")
logv = lvero(final)
grad = score(final)
VC = -inv(H)
print("Log-verosimilitud final\n",logv,"\nValor del gradiente final\n",grad,
"\nMatriz de covarianzas estimada\n",VC,"\n Valores estimados\n")
return(final)
i = i+1
inicial = final
print("El algoritmo Newton-Raphson podría no converger\n",
"Se encontraron problemas de convergencia\n",
"El algoritmo fue detenido")
x0 = [1280,1]
NR(x0)La siguiente imagen muestra el resultado obtenido usando python.

Conclusión
Este algoritmo es my útil para obtener estimaciones y sus intervalos de confianza ya que es muy rápido a diferencia de otros métodos de optimización, por lo que es uno de los más utilizados en estadística.
Sin embargo, es importante mencionar que este método requiere tener buenos valores iniciales, de otro modo el algoritmo podría ser lento o incluso no converger. Otro problema es que es necesario tener las derivadas de las funciones a optimizar, lo cual puede ser un grave problema si la función es muy complicada, por lo que se deberian explorar otras alternativas.
Referencias
Burden, R., & Faires, D. (2002). Análisis numérico (Séptima Edición). Thomson Learning.
Meeker, W. Q. & Escobar, L. A. (1998), Statistical Methods for Reliability Data, New York, NY; John Wiley & Sons.
R Core Team. 2022. R: A language and environment for statistical computing. R Foundation for Statistical Computing. https://www.R-project.org/.
SAS Institute Inc. 2018. SAS/STAT 15.1 User’s Guide. Cary, NC.
SAS and all other SAS Institute Inc. product or service names are registered trademarks or trademarks of SAS Institute Inc. in the USA and other countries. ® indicates USA registration.